MAT511 homework, due Sept. 30, 2009
Let 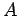 ,
, 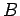 ,
, 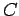 be sets.
be sets.
- Prove that
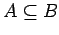 if and only if
if and only if
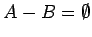 .
.
- Prove that
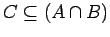 if and only if
if and only if
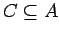 and
and
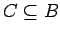 .
.
- Prove that
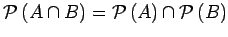 . You
may use the results above.
. You
may use the results above.
- Prove that
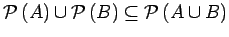 .
.
- Give an example where
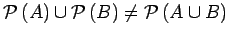 . What conditions
are necessary on
. What conditions
are necessary on 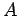 and
and 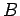 to ensure that
to ensure that
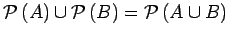 ?
?
- Show that there are no sets
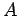 and
and 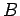 for which
for which
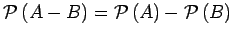 .
.
- Let
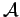 be the family of all sets of integers containing
be the family of all sets of integers containing
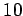 . What are the sets
. What are the sets
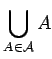 and
and
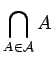 ?
Justify your answer.
?
Justify your answer.
- Let
![$ {\displaystyle A_n = \left[ \frac{1}{n}, 2+\frac{1}{n} \right]}$](img18.png) .
What are the sets
.
What are the sets
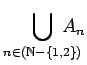 and
and
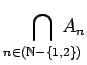 ?
Justify your answer.
?
Justify your answer.
- Let
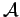 and
and
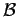 be two pairwise disjoint
families of sets. Let
be two pairwise disjoint
families of sets. Let
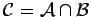 , and
, and
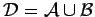 .
.
- Prove that
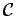 is a pairwise disjoint family of sets.
is a pairwise disjoint family of sets.
- Give an example where
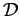 is not a pairwise disjoint
family of sets.
is not a pairwise disjoint
family of sets.
- Prove that if the sets
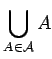 and
and
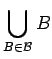 are disjoint, then
are disjoint, then
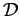 is a pairwise disjoint family.
is a pairwise disjoint family.
Tony Phillips
2006-09-20
![]() ,
, ![]() ,
, ![]() be sets.
be sets.
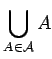 and
and
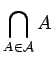 ?
Justify your answer.
?
Justify your answer.
![$ {\displaystyle A_n = \left[ \frac{1}{n}, 2+\frac{1}{n} \right]}$](img18.png) .
What are the sets
.
What are the sets
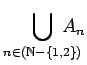 and
and
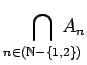 ?
Justify your answer.
?
Justify your answer.
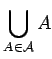 and
and
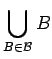 are disjoint, then
are disjoint, then