Another very commonly encountered fractal is the Sierpinski gasket, which can be described as follows:
We start with an equilateral triangle ![]() , and replace it by
three equilateral triangles with a base half the size of the original,
stacked so the original perimiter is kept, but leaving a hole in the
center. We then replace each of those triangles by three more
triangles, to obtain
, and replace it by
three equilateral triangles with a base half the size of the original,
stacked so the original perimiter is kept, but leaving a hole in the
center. We then replace each of those triangles by three more
triangles, to obtain ![]() as nine triangles, each with a base
of length 1/4. Continuing in this fashion
infinitely many times yields the Sierpinski gasket
as nine triangles, each with a base
of length 1/4. Continuing in this fashion
infinitely many times yields the Sierpinski gasket ![]() . The
sets
. The
sets ![]() through
through ![]() are shown below.
are shown below.
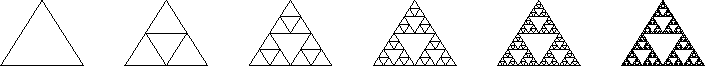
It is easy to see that
![]()
![]() is
ln 3/ln 2, or
about 1.58. You should try to confirm this fact for yourself. The
self-similarity of the Sierpinski gasket should help this
calculation considerably.
is
ln 3/ln 2, or
about 1.58. You should try to confirm this fact for yourself. The
self-similarity of the Sierpinski gasket should help this
calculation considerably.
How might we coerce our turtle into making a Sierpinski gasket?
While the procedure is simple enough to describe, explicitly writing
it down in symbols requires a bit of thought. Give it a try before
continuing.
One way to accomplish this5.18involves taking a slightly different viewpoint. Rather than making
the gasket by replacing triangles with smaller triangles, we construct
a fractal ``curve'' that traverses the base and the perimeters of the
``holes''. This traces out the same sets ![]() , except for
two segments which we can easily add later.
, except for
two segments which we can easily add later.
We view S0 as the straight horizontal segment F, along with two other segments which are not horizontal. To emphasize the difference between the horizontal and the non-horizontal segments, we will traverse the non-horizontal segments backwards, and use the command B. Thus, our first triangle is S0 = FRBLLB.
Now, to obtain S1 from S0, we replace the horizontal segment F by
two smaller ones with an inverted triangle between them. As with
S0, we use F to denote the horizontal parts and B for the
non-horizontal portions. Thus, we apply the transformation
F ![]() SF RBLFLBR FG. This gives us S1 from
S0 as the command ``SF RBLFLBR FG RBLLB''. If we replace all three
Fs in S1 using this transformation, we will obtain S2.
SF RBLFLBR FG. This gives us S1 from
S0 as the command ``SF RBLFLBR FG RBLLB''. If we replace all three
Fs in S1 using this transformation, we will obtain S2.
Before we try to describe any of the Sn recursively, note that in this description, each one really consists of two pieces: there is the complicated, recursive portion which describes most of the gasket, and then there is the final RBLLB which makes the outer ``hat'' (see figure 4). Let's call the commands to produce this first part sn and call commands for the hat h, that is, Sn = sn h. Then we can describe Sn as follows
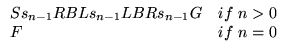 h = RBLLB.
h = RBLLB.
 |
As in the previous sections, once we have worked out the algorithm,
writing the maple code to implement it is quite straightforward. We
we will use the name Sierp for the procedure that produces
sn, and Sierpinski for the procedure to produce Sn.
>
Sierp:=proc(n::nonnegint)
if (n=0) then
`F`;
else
cat(`S`,Sierp(n-1), `RBL`, Sierp(n-1), `LBR`, Sierp(n-1), `G`);
fi;
end:
>
Sierpinski:= n -> cat( Sierp(n), `RBLLB`):
Since we also need to set the angle and scale appropriately, we can
combine them all into a single command DrawSierp:
>
DrawSierp:= proc(n::nonnegint)
SetTurtleAngle(60);
SetInitTurtleHeading(0);
SetTurtleScale(.5);
TurtleCmd(Sierpinski(n));
end:
>
DrawSierp(9);

Warning: Drawing even ![]() takes a significant amount of time and is
almost indistinguishable from
takes a significant amount of time and is
almost indistinguishable from ![]() . If you try to draw
. If you try to draw
![]() , be prepared to wait quite a while, and make sure your computer
has plenty of memory.
, be prepared to wait quite a while, and make sure your computer
has plenty of memory.