Fitting a cubic to data

Let us now try to fit a cubic polynomial to some data. We do so directly, without using Maple's built-in fitting package.

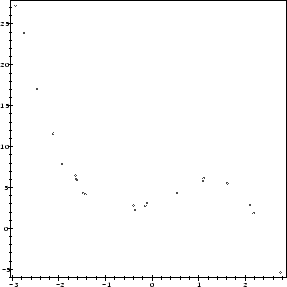
We randomly generate a set of 21 data points to be fitted to a cubic using a Maple program. (Don't worry about how this program works just now. We'll get into those details later).

> 
  Seed:=readlib(randomize)():
  with(stats):
  myrand := (a,b) -> evalf(a+(b-a)*(rand()/10^12)):
  points_wanted := 21:

> 
  cubic_pts := proc()
    local fuzz, a, b, c, d,s,x,i;
    a:= myrand(-3,3);
    b:= myrand(-3,3);
    c:= myrand(-3,3);
    d:= myrand(-10,10);
    if (myrand(-10,10) > 0) then s:=1 else s:=-1 fi;
    fuzz := [ random[normald[0,0.5]](points_wanted)];
    x    := [ random[uniform[-3,3]](points_wanted)];
    RETURN([seq([x[i],s*(a-x[i])*(b-x[i])*(c-x[i])+d+fuzz[i]],
                i=1..points_wanted)]);
  end:

Now we can put the data to be fitted into a list, and visualize the result with plot:

> 
  data:=cubic_pts():
  plot(data, style=point, axes=boxed);

Now we have a set of 21 data points which are to be fitted to a cubic polynomial. A polynomial function of degree n is determined by n + 1 coefficients. So we define

> 
  cub := (x,a,b,c,d)->a*x^3+b*x^2+c*x+d;

and then define the error function:

> 
  E:=(a,b,c,d,data)->sum((cub(data[i][1],a,b,c,d)-data[i][2])^2,i=1..nops(data));

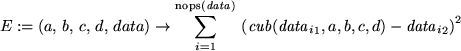
We have four parameters to determine, the coefficients of the function cub. We find its values by

> 
  assign(solve(diff(E(a,b,c,d,data),a)=0,
                diff(E(a,b,c,d,data),b)=0,
                diff(E(a,b,c,d,data),c)=0,
                diff(E(a,b,c,d,data),d)=0,
               a,b,c,d));

Of course, we do not see the answer, but the resulting values have already being assigned to the coefficients a, b, c, d:

> 
  cub(x,a,b,c,d);

Finally, let's make a picture of the result, showing both the data and the fitted curve:

> 
  with(plots):
  cplot := plot(cub(x,a,b,c,d), x=-4..4, axes=boxed):
  pplot := plot(data, style=point):
  display(cplot,pplot);

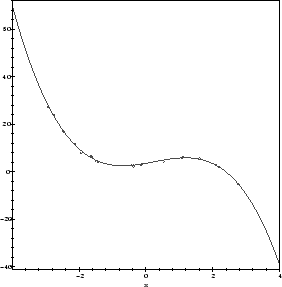
For comparison, let us find the answer using Maple's built-in statistical package:

> 
   with(CurveFitting):
   LeastSquares(data,x,curve=A*x^3+B*x^2+C*x+D);

For this particular version of least square fitting, we may once again interpret the error function E geometrically as the square of the Euclidean distance between a$\vec{x}_{3}^{}$ + b$\vec{x}_{2}^{}$ + c$\vec{x}_{1}^{}$ + $\vec{d}$ and the vector $\vec{y}$, where $\vec{x}_{j}^{}$ = (x₁^j, x₂^j,..., x_n^j), $\vec{d}$ = d (1, 1,..., d ) and $\vec{y}$ = (y₁,..., y_n). The best fit is thus achieved when the coefficients a, b, c and d are chosen so that a$\vec{x}_{3}^{}$ + b$\vec{x}_{2}^{}$ + c$\vec{x}_{1}^{}$ + $\vec{d}$ is the orthogonal projection of the vector $\vec{y}$ onto the subspace of $\R^{n}$ spanned by $\vec{x}_{3}^{}$, $\vec{x}_{2}^{}$, $\vec{x}_{1}^{}$ and (1, 1,..., 1). That is to say, the best fit occurs when the vectors $\vec{y}$ - (a$\vec{x}_{3}^{}$ + b$\vec{x}_{2}^{}$ + c$\vec{x}_{1}^{}$ + $\vec{d}$) and a$\vec{x}_{3}^{}$ + b$\vec{x}_{2}^{}$ + c$\vec{x}_{1}^{}$ + $\vec{d}$ are perpendicular. You should verify that this is the case for the solution given above.

In both cases, you should consider why there is only one critical point for the error function, and why it is of necessity a global minimum.