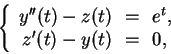
with initial conditions:
For ![]() taking all integer values from -10 to 10, and
taking all integer values from -10 to 10, and ![]() , plot the functions
, plot the functions ![]() in blue, and the functions
in blue, and the functions ![]() in red, all on the same graph. (Yes, you will then have 42 functions
plotted on the same graph.)
[This is certainly a case when you don't want to retype the
functions that Maple finds.
You will almost certainly need to read the help page for
dsolve.
I also found
subs,
unapply, and
seq useful.]
in red, all on the same graph. (Yes, you will then have 42 functions
plotted on the same graph.)
[This is certainly a case when you don't want to retype the
functions that Maple finds.
You will almost certainly need to read the help page for
dsolve.
I also found
subs,
unapply, and
seq useful.]
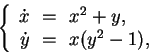
find the eigenvalues and eigenvectors of the Jacobian at the fixed points.